So, in between games of Defense of the Ancients and the Warcraft III expansion campaign, I've been trying to figure out what causes those wildly deviating data points. One possibility is that it's context switches, either due to another thread getting the CPU (time-slicing), or to servicing of an interrupt. Skywing pointed out to me that only administrators may set threads to real-time priority (which disables time-slicing), and as a non-administrator, Windows will silently make real-time priority requests to highest priority (significantly higher than normal priority, so it will get virtually all of the CPU, but is still subject to time-slicing). And even real-time threads may be interrupted by a hardware interrupt *cough*
However, this doesn't explain the change in proportions between no cutoff and 50,000 cycle cutoff. The probability of an interrupt occurring while your thread is running is proportionate to how long your thread is running, meaning that, on average, the proportions should be the same, regardless of how long your thread runs for (this isn't strictly true for time-slicing, but I believe the alternate situation does not apply in this case, due to the extremely high priority of the benchmark thread, and the frequent "rest stops" the benchmark thread takes, to theoretically eliminate time-slicing).
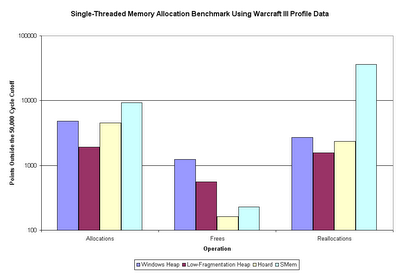
Something that is interesting to note is that I just did a sum using a cutoff of 15,000. While this caused a moderate increase in speed, the proportions (ratios of one data series to another) remained almost identical to when a 50,000 cycle cutoff was used. This tells me that, regardless of whether the 50,000 cycle cutoff is too low, it's definitely not too high. The difference in times between the 50,000 and 15,000 sums may be due to valid allocations times that are higher than 15,000 cycles (maybe the large allocations? or the later operations?). Or, it could be due to short interrupt service routines getting executed (applying uniformly, as I predicted).
Search This Blog
Wednesday, May 31, 2006
More Thoughts on the Benchmark
Memory Allocator Benchmarks - Take 2.1
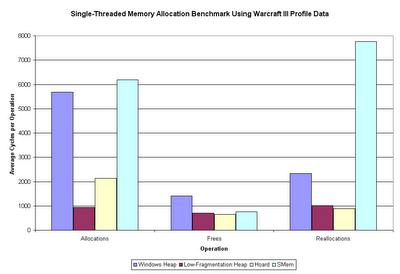
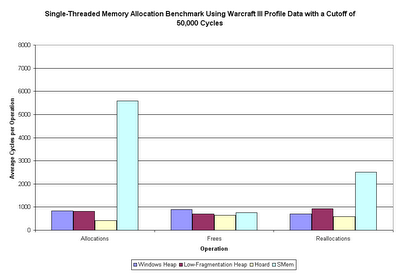
Sweet mother of Kaity - that's more than a little bit different than the first time around. The Windows heap is 7x, 1.5x, and 3x as fast as it was before the cutoff. Other than that, the Hoard allocation speed is about 5x what is was, and SMem reallocation speed is about 3x what it was. All the other categories are no more than 10% different (faster) than what they were originally.
What this tells us is that some operations (the ones just listed) on some allocators have dramatically greater variance in operation time. Exactly which of these two versions is the more accurate, I couldn't really tell you. I'd tend to think the first one (the one including outlier points) would be the more representative of actual usage, although it's more susceptible to outlier points skewing the averages.
Memory Allocator Benchmarks - Take Two (Kinda)
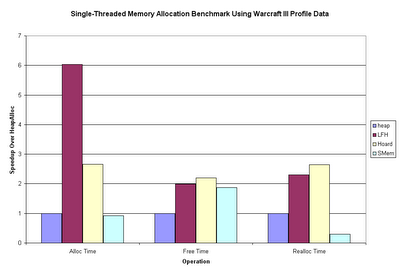
Once again the data speak for themselves, and again they surprised me. Hoard seems like a fairly well rounded choice, though the Windows low-fragmentation heap absolutely owned the allocation benchmark. SMem is, indeed, almost twice as fast as HeapFree, but gets its ass handed to it in the reallocation benchmark.
I'm not sure why SMemReAlloc does so badly. It's possible that it has a larger proportion of outlying data points (points in the hundreds of thousands or millions of cycles) than the others, which could severely skew the results, as this is a sum function. I may try doing the same process using some data point cutoff, and see how that affects the results; though I'm not sure what a fair cutoff point would be.
Oh, and for reference, from what I've heard, the Windows low-fragmentation heap is very similar to the algorithm I was going to implement for LibQ (the lock-free one).
Friday, May 26, 2006
Any-User Program Installation - Part 1
This is done through the Computer Management console (at least in Windows XP), and requires administrator access. Computer Management is located under Administrative Tools, in the Control Panel. If you're not running as an administrator account, you can right click on Computer Management, and click Run as... to run the program as administrator (this is relatively convenient, as it allows you to run programs that require administrator access without changing users).
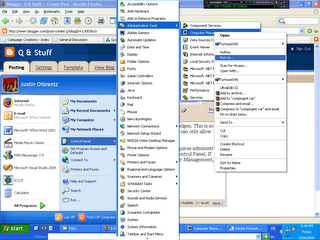
Go to the group list, right click on the list of users, and add a group called Program Installers. Add whoever should be there to the list.
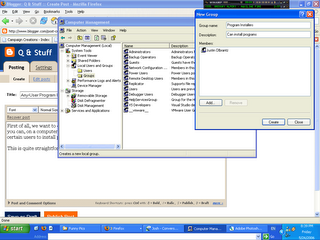
That was trivial. In fact, all of these steps are going to be. I just decided to break them up into separate posts so that if I get lazy and don't feel like finishing the whole series today, I can at least have something to show for it :P
Howto: Installing Programs with Any User
Now, before I say anything more, let me point out that this is only intended to work on programs that are multi-user friendly (that is, they don't assume they can write to their Program Files folder whenever they please). Maybe I'll do a post afterwards about how to deal with those types of programs.
Right now I'm thinking this post series will have the following parts (each one should be pretty brief, as none of them are particularly difficult:
1. Creating a user group for users that can install programs
2. Allowing programs run by users to add to the Program Files folder, start menu, and shared desktop (while not creating a gaping security hole on multi-user systems)
3. Allowing programs run by users to add to the registry (same criteria)
4. (maybe) Having the system take ownership of programs after they're installed (so that one user can't uninstall something that is used by multiple users)
Now, note that, while I have a general idea of how to accomplish this, I've not tried this before; so this will be a learning experience for all of us. We'll deal with complications as they arise (I can already think of one that might come up...).
Wednesday, May 24, 2006
Looks Like I Forgot to Mention Something
Speaking of which, I've managed to gather quite a bit of data with that thing; unfortunately, I don't have a program that works that is capable of graphing several million data points. Mathematica just falls over and dies when I try to open my data files, R bugs out when attempting to graph the data, and SciLab has the tendency to kill my computer. GnuPlot seems pretty nice, but doesn't support regression, for determining complexity. Though at least it can graph the points; I may have to take what I can get :P
Sunday, May 21, 2006
Okay, Enough of That
Saturday, May 20, 2006
**** Me!
So, I randomly decided to rerun MemTest 86 on my computer, following one of its many BSODs, of late. This proved rather... enlightening. The last time I'd ran it on my computer, it was showing one or two invalid bits every run (it was always only on test #7 - random data, which takes about 10 minutes). Today, however, it was finding bad bits at a rate of one every 10 seconds, or so... yeah, that's bad. At that point I wondered why on earth I'd kept using this CPU for so long, and immediately pulled it and replaced it with an old 1 Ghz Athlon, which is currently running MemTest 86 (and will be running some other diagnostics afterwards).
So, why did I (and still do) think that it's a problem with the L1 cache, as opposed to the memory, motherboard, or L2 cache (listed in order from most probable for a memory error)? After running MemTest 86 for several hours (it took that long when it was only generating errors every 10 minutes; now I can get as much info in only 10 or 15 minutes), I noticed that the errors were always at bit 27 of each 32-bit block of memory - the bit was 0 when it should have been 1. The addresses, however, varied widely, and spanned all three of my DIMMs. The probability of this being a memory problem was virtually 0.
However, while there was no relation among the upper bits in the addresses where failure appeared, the pattern in the lower bits was unmistakable: the lowest 16 bits were, without exception, 0x0194 or 0x8194. That is, the lowest 15 bits were identical in all cases.
Now, let's talk about my computer. It's an AMD Athlon XP 2200+. I looked up info on the AMD web site, and found that it had 128 KB of L1 cache, divided into 64 KB data and code caches. Both were 2-way set associative. The L2 cache consists of 256 KB of 16-way set associative cache. This information allowed me to make some predictions for what would happen if a bit was bad in both of them. 256 KB / 16 (-way set associative) would mean that a single bad bit would show up no more than every 16 KB. However, in the L1 cache, 64 KB (data cache) / 2 (-way set associative) means that a single bad bit would show up no more than every 32 KB - the exact pattern that was observed in MemTest 86, and even the same pattern observed in the BSOD crash dumps SW has been sorting through the last couple days.
Interestingly, as previously mentioned, only a single one of MemTest 86's tests showed a problem with the memory - the random number write/read test. All the rest of the tests use heuristics - methods that will detect failures common in memory chips due to the architecture of the chips. Thus it's not surprising that these tests would not be able to detect errors in the cache, with its entirely different architecture. Even still, I find it interesting to see this proven experimentally.
Update @ 6:24 PM: The new CPU has completed one full run of MemTest 86 (took about 1 3/4 hours) with no errors. While that's not a guarantee that it has no problems, it's almost certain that the bad bit problem in the previous CPU is gone, now.
Friday, May 19, 2006
Rootkit Ho?
Seems like he's off on lunch break at the moment, but before that he found that something is hooking the system call table (NtConnectPort, to be precise) and forwarding it to dynamically generated code. In kernel mode. So it's not real surprising that it crashes from time to time. That just leaves the question of WHAT is hooking the call, and WHY.
UPDATE @ 12:58 PM: It's Symantec Antivirus that's doing the rootkit-like behavior. It's not yet known whether that is what's causing the BSODs, though. We're gonna try a virtual sting operation to find out.
UPDATE: It appears to be due to a hardware failure. 1 bit is occasionally being 0 when it should be 1. I believe this to be the same problem I saw with MemTest 86 several months ago. If I recall correctly (I can't find the stuff I wrote down back them), the addresses memory errors occurred at always had the same lower 15 bits, and the upper portion of the addresses was essentially random. This led me to hypothesize that there is a bad bit in the L1 cache. I may need to code (or pirate) an L1 cache diagnostic program.
Thursday, May 18, 2006
The Rotary Set Implementation
The implementation is that of a circular doubly-linked list, but there are a couple tricks to making it work. First, readers only traverse the list in one direction: forward. That means that only the forward links and the head pointer need be kept valid at all times. In fact, I don't even declare the backward pointer in the nodes as volatile.
That brings us down to two variables that must be kept in sync: the forward links and the head pointer. However, with some careful instruction ordering, we find that we don't need to keep the head pointer coherent with the forward links 100% of the time (though the forward links must always be coherent).
The trick is to know where the linearization points are - the points where changes atomically take effect (atomic from the perspective of the readers). In the cases of both the insertion and deletion, this point occurs when we set the previous node's forward pointer to a new location (either the node we just allocated, in the former scenario, or the node after the one we're deleting). So long as this step is performed atomically, the change will be seamless to the readers. In the case of insertion, we have to set up the new node before doing this, of course. We have to, at the very minimum, set the new node's forward pointer to the node we're inserting before. Once that's done, we can link to the new node, and the chain will always be kept coherent in the forward direction.
That just leaves the matter of the head pointer. To save a bit of speed, new nodes are inserted right after the head node. That means we won't need to change the head pointer for insertions (unless the list was empty, in which case it's a trivial matter of setting the head pointer to the new node after we've made the node's links point to itself).
For deletions, however, there's always the chance that the head pointer will be pointing at the node we want to delete. But this is okay. It's okay for the head pointer to point to the node we're deleting, until we actually free the node's memory (and even then we use hazard pointers, in case some thread is still holding a pointer to it). In this case the linearization point just occurs slightly later: when the head pointer gets changed to point to the node after the deleted node. If a reader tries to read the node we’re deleting and then advances the head, it will just move the head to point to the node after the node we’re deleting, which we were going to do, anyway. At no time does a garbage pointer exist anywhere; thus it's fully thread-safe.
So, those are the solutions for the "hard parts". The rest is just vanilla hazard pointers, atomic compare/exchanges, and memory barriers.
Factoid
Wednesday, May 17, 2006
SWMR Rotary Set Ho!
So, what in Kaity's name is a rotary set? Well, I basically made that name up (along with the structure, itself), with the intent of being as descriptive as possible. I don't know if anyone's conceived of this structure before, but I'd be surprised if nobody had. A rotary set is an unordered circular set. Yes, there's a good reason you'd want a circular set. As with normal list-based sets, there is a single head pointer (never mind the fact that it's not actually the head); however, this pointer doesn't always point to the same place. It's called a rotary set because this pointer can revolve around the set, one node at a time - it's as if the circular set is rotating.
Now, what use could such a thing possibly be? Well, I created it to solve a very specific problem. One of the projects on my todo list is to create an audio streaming system for games. As I want this system to take advantage of multiple CPUs wherever possible, that necessitates using an absolute minimum number of mutexes.
One of the central structures in the system is the list of playing streams for decoding. Let's have a little look at the requirements for this list. First, it has to keep track of all playing streams, like a set. However, making the most efficient use of the CPU (especially if you have multiple non-dedicated threads decoding) dictates that you process these streams in a round-robin fashion. You decode an appropriate amount of data on one stream, then move on to the next, stopping when you've used a large enough portion of the CPU (or run out of buffer space for decoded data). Oh, and these decoding threads will be running at maximal priority, to ensure the sound card doesn't ever run out of data to play.
Given these requirements, a little mental math will tell you that protecting such a list with a mutex would be a very bad idea. What if a thread trying to add a new stream to the list (or remove a stream from the list) runs out of CPU time while it's in the mutex? Why, you could have one (or more) high-priority (and in fact hardware-linked) threads blocking for some unspecified period of time. As I mentioned in a previous post, that's BAD.
The SWMR rotary set is my solution. It supports the following operations:
- Get head: gets the value of the head item. O(1). Lock-free.
- Pull head: gets the value of the head item, and moves the head pointer to the next node in the set. O(1). Lock-free.
- Insert: adds an entry to the set in an arbitrary position (decided by the implementation). O(1). Requires writer lock.
- Delete: deletes the specified entry (based on a key) from the set, regardless of where in the set it is. O(N). Requires writer lock.
Lastly, I should note that I haven't yet written the code for it, so I'm not 100% certain it will work. But I've managed to solve the three or four problems I've been able to find with the concept (and don't know of any others, at the moment).
AAAAAHHHHHHHHHH
For those of you familiar with Crypto++, this thing's source is about that bad. There are like 70 header files, and more template use than one person could possibly learn. But I managed to find the places I needed to change to make it use larger block size. Unfortunately, this guy has hard-coded literally more than 2,000 constants (parameters) for different block sizes - 4 KB, 8 KB, and 16 KB. I guess that explains why he hasn't fixed the problem I reported - it'd take even him a few days to add a completely new block size, and he wrote the thing.
I'm officially giving up on fixing this thing myself :P
Monday, May 15, 2006
Here We Go, Again
Sunday, May 14, 2006
For the Curious
Saturday, May 13, 2006
Errata
Whenever you reserve a region of address space, the system ensures that the region begins on an allocation granularity boundary. The allocation granularity can vary from one CPU platform to another. However, as of this writing, all the CPU platforms (x86, 32-bit Alpha, 64-bit Alpha, and IA-64) use the same allocation granularity of 64 KB.
When you reserve a region of address space, the system ensures that the size of the region is a multiple of the system's page size. A page is a unit of memory that the system uses in managing memory. Like the allocation granularity, the page size can vary from one CPU to another. The x86 uses a 4-KB page size, whereas the Alpha (when running both 32-bit Windows 2000 and 64-bit Windows 2000) uses an 8-KB page size. At the time of this writing, Microsoft expects the IA-64 to also use an 8-KB page size. However, Microsoft might switch to a larger page size (16 KB or higher) if testing indicates better overall system performance.
So it seems the mystery of the 8 KB reserved region wasn't really a mystery at all.
As for Hoard, after I reported the issue on the mailing list, the author acknowledged the existence of the flaw earlier today. At the time I was doing the debugging, I guessed (and I still believe) that he's a Unix guy, and so wasn't aware of the quirky way Windows handles allocating memory (that is, the 64 KB allocation granularity). Hopefully he'll fix it pretty soon, because Gord knows I'm too lazy to do it :P
Allocator Benchmark WTF
Hoard, however, is exactly the same as it was in the previous version: not working. It starts failing allocations with about 350 megs allocated, for reasons that can only be described as Outer Limitsish. At 350 megs, my virtual address space is nowhere near full, nor is my physical memory or virtual memory. Yet the author of Hoard swears that Hoard will not fail unless it runs out of memory. The answer turned out to be the weirdest of both worlds.
This is what WinDbg (may I just say that I loathe that stupid program) has to say about the memory state of the program, at the point of the crash (due to new returning NULL and it getting accessed):
-------------------- State SUMMARY --------------------------Okay, so the quantities of committed, free, and reserved memory are about what you'd expect (actually, I would have expected reserved memory would have been a lot higher, but that's relatively unimportant). The real WTF is that last line. When I first saw that, I thought it had to be BS. With 372,224 KB allocated/reserved, the worst-case scenario would be that an equal amount of memory would be diced into 64 KB blocks (this would be one 64 KB allocation unit being committed/reserved, the next free, etc.). That would leave about 65% of the address space completely free, and the largest free block size should be a few orders of magnitude larger than 64 KB.
TotSize ( KB) Pct(Tots) Usage
16507000 ( 365596) : 17.43% : MEM_COMMIT
69470000 ( 1724864) : 82.25% : MEM_FREE
679000 ( 6628) : 00.32% : MEM_RESERVE
Largest free region: Base 00000000 - Size 00010000 (64 KB)
Nevertheless, here's what WinDbg has to say about the virtual address space (a little fragment of it):
68362000 : 68362000 - 0000e000
Type 00000000
Protect 00000001 PAGE_NOACCESS
State 00010000 MEM_FREE
Usage RegionUsageFree
68372000 : 68372000 - 0000e000
Type 00000000
Protect 00000001 PAGE_NOACCESS
State 00010000 MEM_FREE
Usage RegionUsageFree
68382000 : 68382000 - 0000e000
Type 00000000
Protect 00000001 PAGE_NOACCESS
State 00010000 MEM_FREE
Usage RegionUsageFree
68392000 : 68392000 - 0000e000
Type 00000000
Protect 00000001 PAGE_NOACCESS
State 00010000 MEM_FREE
Usage RegionUsageFree
683a2000 : 683a2000 - 0000e000
Type 00000000
Protect 00000001 PAGE_NOACCESS
State 00010000 MEM_FREE
Usage RegionUsageFree
683b2000 : 683b2000 - 0000e000
Type 00000000
Protect 00000001 PAGE_NOACCESS
State 00010000 MEM_FREE
Usage RegionUsageFree
683c2000 : 683c2000 - 0000e000
Type 00000000
Protect 00000001 PAGE_NOACCESS
State 00010000 MEM_FREE
Usage RegionUsageFree
And on it goes, for hundreds of pages. This is just mind-boggling: all these blocks of free space smaller than 64 KB. Querying WinDbg confirms what seems probable from this list: in between each of those blocks are a couple pages of allocated memory.
For those not familiar with Windows memory allocation, there are two levels of allocation: reserve and commit. Reserve reserves a region of the address space, preventing it from being used to allocate memory unless you explicitly tell Windows to allocate from that region. Commit allocates actual memory to the region - either physical memory, or space in the page file. This allows you to, for example, reserve a huge contiguous block of memory for a buffer, but only allocate it as you actually need the memory (e.g. realloc).
Now, reserving is done by the allocation unit, which is usually 64 KB. This means that you must reserve starting at a 64 KB boundary, and reserve some size that is a multiple of 64 KB. Committing is done by the page size - usually 4 KB (note that you can only commit memory out of a reserved region, although you can do both in one system call). That means you can have a 64 KB block that is partially committed and partially reserved. I know of no way to have 8 KB of a 64 KB block committed, and the other 56 KB not reserved (at least not from user mode), and I have absolutely no idea how Hoard has managed to accomplish this. But at least I know what the problem is, so I can get them to fix it.
Tuesday, May 09, 2006
Rebuttal
So, I sent a link to the benchmark to my friend in Blizzard. Surprisingly, it provoked a rather lengthy rebuttal from the "lead of our technology team" (who my friend forwarded my report to). I'm not sure if I'm allowed to post the original e-mail, so I'll just respond to the points in it.
It's true that it's an artificial benchmark. I was looking for a simple and elegant method that would have some resemblance to real-world data. I actually did consider writing a program to record every block of memory something like Warcraft 3 allocates, and then use that as input for my tests. But ultimately laziness got the better of me. Maybe sometime I'll try that.
I honestly hadn't considered the possibility that a memory allocator would be optimized for free time, rather than allocation time, as I expected free to take an almost negligible amount of time (this was why I only benchmarked allocations, because I expected that would be the bottleneck). I might have to do some free benchmarks as well, then.
I'm not quite certain what he meant by SMem being intended for use with multiple heaps (I can think of two possible meanings). I'm aware that SMem also supports the creation of private heaps, although I hadn't seen that used a great deal in my reverse-engineering (though my work is getting pretty dated; I'm not aware what techniques they used currently). If he's referring to slab allocation, that's great; that's the way to optimize allocation performance (which is why I added it to LibQ). This would, of course, produce drastically different results than the benchmark did; of course, it would also produce different results for HeapAlloc and Hoard (at least, if Hoard can do multiple heaps).
The other possibility is that he's referring to the global Storm heaps. For global allocations, Storm uses a set of 256 different heaps, each protected by a separate mutex. Which heap is used is based on the hash of a tag string for each allocation (typically this is either __FILE__ or the decorated name of the structure being allocated). I hadn't really thought that this was to promote similarity of data in each heap; I was thinking it was more to ensure that any two threads would virtually never lock the same heap at once. But if that's the case, it is conceivable that that could influence the results, as there might not be an even distribution of sizes, given the huge number of heaps.
The average block size was 256 bytes. The allocations were randomly chosen from 1 to 512 bytes, with equal probability. While equal probability may not be realistic, it might have been a good thing, given that I couldn't have imagined the bizarre shape of the SMemAlloc "curve" on the graph :P The reason for using numbers this small was based on the assumption that larger allocations would be fairly infrequent, so not as important, performance-wise (and very large blocks getting allocated from the OS). I was actually worried that I might skew the data in unrealistic ways if I made the maximum size any larger.
This was exclusively a single-threaded benchmark by design. There were two reasons for this, one being obvious: I don't have a multiprocessor system :P The other was that multiprocessor benchmarks are fairly common (i.e. on the Hoard site), and so didn't really justify a benchmark (remember that finding problems with Storm wasn't the original goal of the benchmark). That and the fact that multithreaded performance is relatively predictable: Vanilla HeapAlloc is going to do terribly (due to having a single heap mutex), Storm is going to be very fast (due to more or less never having allocation collisions). In fact, the allocator I'm working on is highly scalable (completely lock-free, and actually somewhat resembles the Windows low-fragmentation heap), but I also expected it to be faster than typical allocators for individual allocations (hence the survey of the competition).
Lastly, speaking of the Y axis of the graph, you might find this graph interesting, in which I uncapped the Y axis (I had manually capped it to give the best view of the data) :P
Allocator Benchmark
The test consisted of 7.5 million memory allocations (actually, Hoard only did 2.25 allocations, as that's all I could get it to do before crashing), of sizes ranging from 1 byte to 512 bytes; the total allocation size was generally around 400 MB (although this is a bit misleading, as explained later). A size was chosen randomly from that range, using a PRNG with a constant seed (to ensure reproducibility), and allocated with the corresponding function, each call benchmarked with the Pentium cycle counter instructions. Allocations were grouped into batches of 250, which were executed in real-time priority class (in other words, no thread time-slicing), with the thread sleeping after each batch (to prevent starvation of other threads). For the special case of SMemAlloc, the tag string of "BlubberyKaity" (an inside joke) was used, which I thought was a realistic length for the hashing function to chew on.
Approximately every 256 allocations, a purge was performed. Purges consisted of the freeing of 40% (this exact number is higher than I originally intended to use; it was used to prevent running out of physical memory on the test computer, while keeping the number of allocations the same) of the currently allocated blocks, chosen randomly. This was done as a crude attempt to simulate how memory freeing is often done in batches, after the completion of some task that required memory allocations.
At the moment the final memory allocated numbers are misleading, as they are the virtual memory space used at the end of the program run. This would naturally include the memory allocated for the trees used to hold the list of memory allocations (for frees and statistic gathering), and I would imagine they'd take up at least half that number.
HeapAlloc demonstrates a roughly O(log N) curve (where N is the allocation size). HeapAlloc, when using the low-fragmentation heap option, displays approximately O(1) complexity. The Hoard curve has a rather peculiar shape, and it's difficult to characterize it before around N = 280, where it seems to adopt a O(log N) shape. By far the strangest is SMemAlloc. From approximately N = 40 to 240, it seems to have a roughly O(1) shape, with a notable amount of inconsistency, despite very clear clustering. It appears that, for N = 0 to 40 and N = 240+, I takes on a O(x^N) shape (this is definitely true for the latter case, although the former range is fairly small to draw conclusions from).
It's also noteworthy to point out that Hoard worked a bit differently than the other allocators. Save for Hoard, all of them operated on private heaps (heaps that didn't have the allocation tracking stuff allocated from them). In the case of Hoard, I was only able to get it to work by letting it hook malloc and new (what it does by default). Consequently, all allocations, even ones not part of the test, were performed using Hoard. I don't know whether this may have biased the results, or in which direction.
Monday, May 08, 2006
Wooooow
- When there is nothing but allocations, HeapAlloc/malloc/new appear to be O(log N) with respect to block size
- When there is a significant amount of deletions intermixed with allocations, HeapAlloc/malloc/new are O(1), and actually as fast or faster than HeapAlloc/malloc/new with allocations only (big surprise)
- HeapAlloc from a private heap is O(log N), faster than HeapAlloc from the global heap for allocations <> 100 bytes (also a big surprise).
- SMemAlloc is just about the biggest POS ever coded. By about 50 byte allocations it passes HeapAlloc/malloc/new, and continues in what appears to be O(N) (it's really hard to tell, because the data is all over the freakin' place; it could also be O(log N)). At 320 bytes, it becomes O(x^N), getting up to around 100 K cycles for 500 byte allocations. I know that's my shock and awe for the day.
Saturday, May 06, 2006
To Skew or Not To Skew - Part 2
It looks like my analysis of this lock-free priority queue was right on the money: the algorithm can be quite inefficient (about half as fast as the priority queue using a spin-lock). It seems that Herlihy (the guy who wrote the algorithm) did a fair bit of research on it back in 1993. He also managed to identify a solution to the problem: exponential back off.
While the article doesn't do benchmarks on the skew heap with exponential back off, the normal heap with exponential back off shows a remarkable increase in speed, performing superior to the spin lock version beginning at about 6 threads executing concurrently. At 16 processes contending for the same priority queue, the lock-free heap with exponential back off is about twice as fast as the spin lock version.
However, using exponential back off with the spinlock gets faster, still. The heap using a spinlock with exponential back off is about 65% faster than the lock-free heap with exponential back off.
Last, it should be noted that there's an inherent bias in these results. They all use artificial situations where memory access is minimized in the case of the spin lock version, so most of the access can be done from cache, in contrast to the lock-free algorithm. So it's possible that in real world scenarios the lock-free version will be faster, relative to the spin-lock version.
So, we got some nice information, but it really doesn't answer the question of whether I should implement this sucker :P
Friday, May 05, 2006
Goin' for the Gold!
So, that brings us to the third and final item on the list of lock-free thingamajiggers I wanted to add to LibQ (excluding the allocator; that thing is tricky to implement; I'll get around to that at some point): the atomic deque. And I've got a serious problem.
The algorithm requires the use of atomic memory writes larger than one word. This is something which, of the architectures I want LibQ to support, only x86-32 supports, making it highly impractical.
There are two ways to get around this. If you remember, I have this little thing called CAtomicVar, which allows atomic operations on types larger than one word, for a price: one memory allocation each time the variable is written to (typically this will be twice per push/pop, although in periods of high contention it may be more than that). A third allocation will be required for push operations.
That's pretty bad. Even with a free list allocator I'd wager that's at least 100 cycles inside the window of invalidation vulnerability, considerably more without a free list.
The other solution is to make the deque fixed size - it can only hold so many items, maximum. That's not all; this method will only work on CPUs that can atomically access 64-bit values. This is only supported on x86 and PPC64 (G5, I think) CPUs, leaving most Mac users out.
So, that's the problem, and those are the solutions. This brings up the question: is it worth it? If so, which method is better?
To Skew or Not To Skew
Two dilemmas in one day; how about that? This one is about this algorithm for a lock-free skew heap. Figuring out how this thing works just from the pseudo-code was a bit tricky, but I think I've got it, now. It works by reallocating every node it modifies in the skew merge, creating a partial duplicate in memory (recycling nodes where possible), then finally atomically activating the new tree by swapping out the root node.
So, that means about O(log N) allocations per enqueue/dequeue operation. This thing keeps its own free list of nodes, so allocations are relatively fast. Though I'm still a little worried. I can't imagine this thing taking less than a few hundred cycles to perform an operation (when there are 10 or 20 nodes), and if another thread modifies the tree while the operation is in progress, the entire operation gets discarded, and it tries again. That's an awfully hefty penalty for failure.
I'm not sure if it'd be better to write the thing and let it gobble up cycles when there's contention, or just leave you to use a mutex with a non-lock-free priority queue. With the other lock-free structures thus far, most of the time (allocating memory, etc.) can be done without any chance of it going to waste, as the window for another thread invalidating your work is very small (only a couple dozen cycles, and only the work done in that window will get invalidated if another thread gets there first). Here, the window is quite large; there's only so much you can do outside the window ahead of time (like maybe allocate plenty of memory to the free list so that you can be sure the list will be large enough to get you through the window; but even if you did you'd probably still have a window of a couple hundred cycles).
Put in more of layman’s terms, there isn't as much to gain from a lock-free priority queue as there is for the other lock-free structures.
To Wait or Not To Wait
So, I've been looking over these atomic structure algorithms (the ones I didn't implement already) again, now that I've got some relatively free time. I'm really having a hard time deciding whether to implement the wait-free variable.
The wait-free variable does exactly what the atomic variable does, only better: allow load/store with reserve, exchange, unconditional set, etc. The problem is that, like all the other atomic structures, the atomic variable is implemented with compare/exchange loops. This means that if there are a large number of threads setting that variable within a short period of time, a thread may have to spin for a while before it gets its turn to read the variable (one spin per thread that writes to the variable).
The wait-free variable partially circumvents this, allowing reads to be performed in constant time, regardless of how many other threads are trying to write to the variable. Writes, however, must still use compare/exchange loops (no way around that).
So, is it worth doing, or not?
Thursday, May 04, 2006
Very Squishy
I mentioned a few weeks ago that I had an algorithm for a lock-free memory allocator. I actually didn't look much at the algorithm for it until today, but it's pretty straightforward; allow me to make you drool a bit.
As mentioned previously, it's lock free. As with all lock free structures, that means that wasted cycles due to competition for it will be very low, even when many threads are trying to use it at once.
But the big deal is that it's zero fragmentation. Fragmentation is what happens when a small block gets freed, when there is still data allocated on both sides of the block. The block can now be reused, but only for requests for blocks the same size or smaller. This can have two bad effects. First, it can wear down your memory over time, by progressively creating smaller and smaller holes. At some point these holes cease to be useful, and they wind up being unusable allocated space. Second, it means that you have to keep a sorted list of free blocks, and go searching through it every time you need a block, to see if you can find one large enough; this makes allocations O(N) with respect to the number of free blocks.
Having a no fragmentation heap means that you can kiss both problems goodbye. You can run this thing for all eternity and you won't have any fragmentation. It's possible (if not probable) that some memory will still go unused, but that's simply because demand for blocks of a given size varies; if demand really high at one point, a bunch of memory will be allocated, and when demand drops, some of that memory will go unused. This isn't the same thing as fragmentation; the memory is still just as useful as the first time it was allocated, it just isn't being used.
Not only that, but I've got three words for you: constant time allocation. No matter how much you use this thing, it'll always be just as fast to allocate memory. Even better, this constant time is very low; likely significantly faster than a single call to malloc (the default implementation, anyway). It doesn't get much better than this.
However, there's a caveat. The simplest and surest way of implementing a zero-fragmentation allocator (and indeed what this one uses) is with a simple trick: you have separate heaps for memory of different sizes, and round allocations up, so that all blocks in a single heap are of the same size. This makes it inherently wasteful (at least when the blocks getting allocated aren't exactly the size of each block of the heap). The amount of waste may be tweaked by how you slice up your heaps. I'll have to do some playing around with this. Here's what I'm thinking at the moment for heap block sizes (note that I haven't spent much time thinking about this yet; I'm basically coming up with these numbers as I type):
- one heap for each power of two and 1.5x each power of two from 32 bytes to 8 KB
- one heap for 1, 1.25, 1.5, 1.75x each power of two from 8 KB to 64 KB
- anything larger than 64 KB gets allocated directly by the OS (VirtualAlloc, etc.)
More or less that means that for blocks 32 bytes to 8 KB, no more than 1/2 of the requested size will be wasted. For blocks 8-64 KB no more than 1/4 of the requested size will be wasted.
Increasing the number of heaps would serve to reduce the waste, but be aware that all allocations will have to locate the correct heap. That means it will do a binary search on the table of heaps, which takes O(log N) time. Also, increasing the number of heaps wastes memory in another way: all memory must eventually be allocated from the OS in large (probably 64 KB) blocks. Each heap that has at least 1 item allocated at some point will have one of these blocks associated with it. If you have a 64 KB block of memory that only has a single 32 byte allocation, that's a rather catastrophic (percentage-wise, anyway) waste of memory. On the other hand, if you're writing something like World of Warcraft, which allocates hundreds of megs of memory of widely varying sizes, a few megs of wasted space for unused blocks (1 megs would be 16 heaps) is probably worth it. So, I'll probably allow you to tweak the heap organization for your own projects as needed.
Wow, that post turned out to be way longer than I expected. Story of my life, I guess...
Tuesday, May 02, 2006
& More Good Anime
& Random Thoughts
Like a disturbance in a quiet pond, the sounds of pandemonium rippled outward from ground zero in a series of precisely ordered events. First, the sounds of glass shattering and sheered sheet metal landing on concrete, then the sounds of car alarms going off, and, finally, such assorted screams as "My Cresta!" and "The roof is on fire!"A short passage from one of my apocryphal stories (that is, a story that could never happen, as it doesn't fit in any universe, though it interacts with various ones) that is an anime grand melee crossover. The ground zero mentioned would be Kaolla's jet engine blowing up during its test run.
Monday, May 01, 2006
& Public Service Announcements
*loads shotguns*


