The Solution

Alright, let's see if I can get through writing this post without my computer blue-screening (again).

The reason this question was so cool is that it's not only hard (1 in 25 isn't very much), but the solution is extremely simple and elegant (at least in concept; when written out in grammar it isn't so pretty): it's a simple deterministic 4-state machine, represented by the following graph:

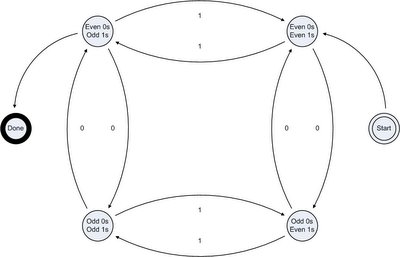
The machine begins in the even 0s and even 1s state, and changes state each time it reads a bit in the number (the order it does this doesn't matter). If at the end of the string the state is even 0s and odd 1s, then the number is valid. This machine can be directly expressed in grammar, but it can be a bit cumbersome to read; thus why I've only given the graph.

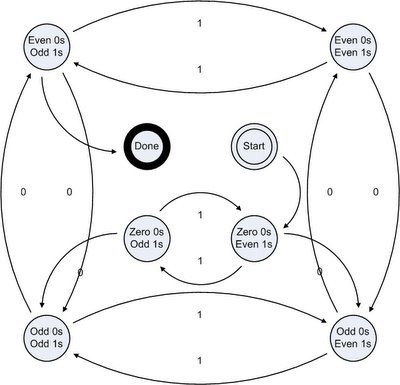
As a bonus, this next graph shows a machine for the same problem, save that it's 0-exclusive: it isn't valid to have zero 0s and odd 1s.

Oh, and on an unrelated note, I just learned that Windows Vista has new API functions for read-write locks and condition variables. Also, NT 3.5+ has undocumented but stable functions for read-write locks. I'll have to see about adding support for those in LibQ at some point (heck, I'll have to see about doing anything with LibQ at some point). For those of you wondering, the complete lack of content lately has been due to me getting back into WoW after a couple month break :P